Virhemarginaalilaskurin kaava ja esimerkkejä
Näin lasket virhemarginaalin ja mittaat sitä tarkalla verkkolaskurillamme.
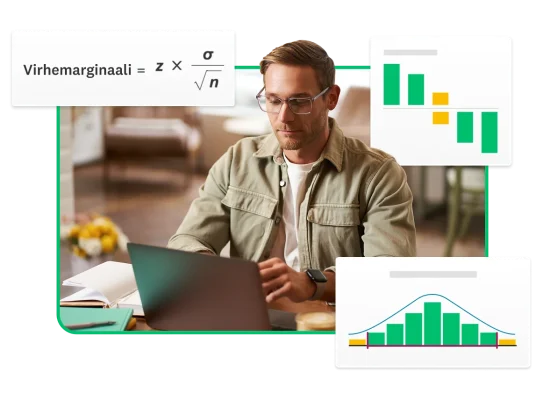
- Virhemarginaali kuvaa kyselytutkimustulosten epävarmuutta osoittamalla, kuinka paljon otoksesta saadut tulokset voivat poiketa koko populaatiosta.
- Virhemarginaali lasketaan näillä elementeillä: n = otoskoko • σ = populaation keskihajonta • z = z-tulos (voit myös käyttää laskuria alla).
- Virhemarginaalin laskurilla selvität, onko otoskokosi riittävä, jotta voit luottaa keräämäsi datan tarkkuuteen.
Laske virhemarginaali
Populaation koko
Luotettavuustaso (%)
Otoskoko
Virhemarginaali
0
Virhemarginaali
Kyselytutkimuksissa pieni joukko (vastaajat) edustaa paljon suurempaa joukkoa (kohdemarkkinoita tai koko populaatiota). Virhemarginaali on tilastotieteellinen mittari, joka kertoo, kuinka tarkasti kyselytutkimuksen tulokset vastaavat koko populaatiota.
Virhemarginaalilla mitataan kyselytutkimuksen tarkkuutta. Pieni virhemarginaali tarkoittaa tulosten olevan luotettavia, ja vastaavasti mitä suurempi virhemarginaali on, sitä enemmän tulokset poikkeavat koko populaatiosta.
Virhemarginaali on kyselytutkimuksen tuloksiin perustuva arvojoukko. Sanotaan esimerkiksi, että kyllä-vastauksia on 60 %, virhemarginaali on 5 % ja luottamusväli 95 %. Tällöin on 95 %:n todennäköisyys, että 55–65 % populaatiosta vastaa ”kyllä” samaan kysymykseen.
Virhemarginaali kertoo tulosten luotettavuudesta, minkä vuoksi se on tärkeä tekijä kaikenlaisissa tutkimuksissa. Se auttaa sekä selvittämään tuloksiin liittyvän epävarmuuden että tulkitsemaan dataa. Pieni virhemarginaali merkitsee tarkkoja ja luotettavia tuloksia, kun taas suuri virhemarginaali kertoo laajemmasta vaihtelevuudesta ja epävarmuudesta.
Virhemarginaali auttaa tutkijoita ja päätöksentekijöitä tekemään perusteltuja päätöksiä datan luotettavuuden mukaan.
Luottamusväli
Luottamusväli auttaa arvioimaan alueen, jolla uskomme todellisen tuloksen olevan. Jos esimerkiksi olemme arvioimassa koko maan kaikkien aikuisten keskimääräistä pituutta, luottamusväli antaa pituuksien arvojoukon, jonka voimme melko varmasti sanoa sisältävän todellisen keskiarvon.
Luottamusväli antaa tutkijoille ja päätöksentekijöille käsityksen heidän arvioidensa ja analyysiensä epävarmuudesta.
Näin virhemarginaali liittyy luottamusväleihin
Luottamusväli ja virhemarginaali ovat periaatteessa kaksi eri tapaa ilmaista sama asia eli kyselytutkimusarvion epävarmuustaso. Luottamusväli antaa arvojoukon, jolla voimme luottaa todellisen arvon olevan, kun taas virhemarginaali mittaa tarkasti, kuinka paljon arvio saattaa poiketa todellisesta arvosta.
Tähän liittyvä mutta eri käsite on luotettavuustaso, joka ilmaisee varmuuden siitä, että todellinen arvo on kyseisellä välillä.
Yleisimmin käytetyt luotettavuustasot ovat 90 %, 95 % ja 99 %. Esimerkiksi matala 90 %:n luotettavuustaso antaa kapean luottamusvälin. Mitä kapeampi väli on, sitä tarkempi arviomme on, mutta matala luotettavuustaso ei ehkä yhtä todennäköisesti sisällä todellista arvoa. Sitä vastoin esimerkiksi 99 %:n luotettavuustaso laajentaa luottamusväliä. Laajempi väli ei ole yhtä tarkka, mutta todennäköisemmin sisältää todellisen arvon.
Virhemarginaalin käyttö
Virhemarginaalia kannattaa käyttää kyselytutkimuksia suunniteltaessa tarkkojen ja luotettavien tulosten varmistamiseksi. Se auttaa laskemaan tarvittavan otoskoon sen mukaan, kuinka tarkkoja haluat kyselytutkimustulosten olevan: pieneen virhemarginaaliin tarvitaan suuri otoskoko ja päinvastoin.
Jos esimerkiksi halutaan tutkia 100 000 ihmisen populaatiota ±5 %:n virhemarginaalilla ja 95 %:n luottamustasolla, otoksessa olisi oltava noin 383 vastaajaa vakiokaavoilla laskettuna.
Tämän lisäksi virhemarginaali on olennainen tekijä kyselytutkimusten tulosten tulkinnassa, koska sillä mitataan tulosten epävarmuutta ja arvioidaan päätelmien luotettavuutta.
Jos esimerkiksi kyselytutkimus on selvittänyt, että 60 % vastaajista pitää tuotetta A parempana kuin tuotetta B virhemarginaalin ollessa ±3 % ja luottamustason ollessa 95 %, on hyvin todennäköistä (95 %), että todellinen osuus populaatiosta, joka pitää tuotetta A parempana, on 57–63 %.
Virhemarginaalin laskentakaava
Virhemarginaali lasketaan tällä kaavalla:

n = otoskoko • σ = populaation keskihajonta • z = z-pistemäärä
- Selvitä populaation keskihajonta (σ) ja otoskoko (n). Keskihajonta perustuu p(1-p):n neliöjuureen, jossa p on otoksen suhteellinen osuus ja p = 0,5 on oletusarvoisesti varovainen arvio.
- Laske neliöjuuri otoskoosta ja jaa populaation keskihajonta tällä neliöjuurella.
- Kerro tulos seuraavan taulukon z-tuloksella, joka vastaa haluamaasi luottamustasoa.
| Haluttu luotettavuustaso | z-pistemäärä |
| 80 % | 1,28 |
| 85 % | 1,44 |
| 90 % | 1,65 |
| 95 % | 1,96 |
| 99 % | 2,58 |
Esimerkki virhemarginaalin laskelmasta
Sanotaan, että yrität valita nimen uudelle tuotteelle kahdesta vaihtoehdosta. Kohdemarkkinoillasi on 400 000 potentiaalista asiakasta, mikä muodostaa koko populaatiosi.
Päätät tehdä kyselytutkimuksen 600 potentiaaliselle asiakkaalle, mikä muodostaa otoskokosi.
Tulokset saatuasi huomaat, että 60 % vastaajista sanoi pitävänsä nimestä A. Sinun on nyt lisättävä luottamustaso virhemarginaalilaskuriin.
Tämä luku ilmaisee, miten varma voit olla siitä, että otos vastaa tarkasti koko väestön mielipidettä. Tutkijat asettavat sen yleensä 90, 95 tai 99 prosenttiin.
Kun syötät tämän esimerkin luvut virhemarginaalilaskuriin, saat virhemarginaaliksi 4 %.
Kuten muistat, 60 % vastaajista piti vaihtoehdosta A. Tämä virhemarginaali tarkoittaa 95 %:n tarkkuudella, että 56–64 % koko populaatiosta (kohdemarkkinoistasi) valitsisi nimen A tuotteellesi.
56 ja 64 saadaan lisäämällä ja vähentämällä virhemarginaali otoksesi vastauksesta.
Näin tulkitset virhemarginaalia
Virhemarginaali antaa kyselytutkimusarvioon perustuvan arvojoukon, joka osoittaa epävarmuustason. Jos esimerkiksi 60 % kyselytutkimuksen vastaajista suosii tiettyä käytäntöä, kun virhemarginaali on ±4 % ja luottamustaso 95 %, voimme luottaa kohtuullisesti siihen, että 56–64 % ihmisistä suosii kyseistä käytäntöä.
Virhemarginaaliin vaikuttavat tekijät
1. Otoskoko
Otoskoko vaikuttaa suoraan virhemarginaaliin kyselytutkimuksissa. Suuret otoskoot merkitsevät tavallisesti pieniä virhemarginaaleja ja vastaavasti pienet otoskoot merkitsevät suuria virhemarginaaleja.
Esimerkiksi 1 000 vastaajan kyselytutkimuksessa virhemarginaali voi olla ±3 %, mutta 2 000 vastaajan otoskoko voi pienentää virhemarginaalin ±2 %:iin.
Aiheeseen liittyvää: Otoskoon laskuri
2. Luottamustaso
Korkea luottamustaso merkitsee suurta virhemarginaalia ja päinvastoin.
Esimerkiksi kyselytutkimuksessa, jonka luottamustaso on 95 %, voi olla ±3 %:n virhemarginaali, mutta jos luottamustaso nostetaan 99 %:iin, virhemarginaali voi nousta ±4 %:iin.
3. Populaation vaihtelevuus
Suuret populaation vaihtelut merkitsevät suuria virhemarginaaleja ja päinvastoin.
Jos esimerkiksi arvioit tuloja kaupungissa, jossa on suuria tuloeroja, virhemarginaalin on ehkä oltava ± 5 000 euroa. Sitä vastoin pienempien tuloerojen kaupungeissa virhemarginaali voi olla pienempi, kuten ± 2 000 euroa.
Näin parannat datan luotettavuutta

Nyt tiedät, miten virhemarginaali lasketaan ja kuinka se vaikuttaa tuloksiin. Katsomme seuraavaksi, mitä sinun on tehtävä voidaksesi käyttää näitä käsitteitä omassa kyselytutkimuksessasi.
1. Määritä koko populaatio
Tämä sisältää kaikki ihmiset, joita haluat tutkia kyselytutkimuksellasi, eli edellisen esimerkin 400 000 potentiaalista asiakasta.
2. Valitse riskitaso
Sinun on valittava hyväksyttävä riski sille, että tuloksesi poikkeavat koko kohdemarkkinoiden asenteista. Sitä varten on mitattava otoksesi virhemarginaali ja luotettavuustaso.
3. Määritä otos
Kun olet valinnut hyväksyttävän luottamustason ja virhemarginaalin, sinun on määritettävä tarvittava vastaajamäärä. Muistathan, että kaikki kyselytutkimuksen vastaanottajat eivät vastaa kyselytutkimukseen, vaan otoskoko tarkoittaa kaikkiin kysymyksiin vastanneiden lukumäärää.
4. Laske vastausprosentti
Vastausprosentti on kaikkien kyselytutkimuksen vastaanottaneiden joukosta se prosenttiosuus, joka on vastannut kyselytutkimukseesi. Voit katsoa tavanomaisen vastausprosentin aiemmista kyselytutkimuksista, mutta jos aiempia tietoja ei ole saatavilla, voit tehdä valistuneen arvauksen. Tavallisesti arvioidaan, että kyselytutkimuksen vastaanottajista 10–15 % vastaa siihen.
5. Kyselytutkimuksen kohdeyleisö
Kun prosenttiosuus 4. vaiheesta on selvillä, osaat lähettää kyselytutkimuksen oikealle määrälle ihmisiä saadaksesi halutun määrän vastaajia 3. vaiheen mukaisesti. Virhemarginaalin (ja muiden tarvittavien tietojen, kuten otoskoon ja luottamustason) selvittäminen kuuluu olennaisesti kyselytutkimuksen suunnitteluun. Kun osaat laskea nämä tekijät, voit jatkaa varmalla pohjalla.
Aiheeseen liittyvää: Populaation arviointi
Paranna virhemarginaalia SurveyMonkeylla
SurveyMonkeylla voit kasvattaa otoskokoa ja pienentää virhemarginaalia. Tehokkaalla SurveyMonkey Audience ‑alustalla voit kerätä laadukasta dataa nopeasti ja vaivattomasti kohdemarkkinoidesi kaltaiselta yleisöltä. Uuden tuotteen lanseeraus, asiakastyytyväisyyden mittaaminen ja akateemisen tutkimuksen tekeminen onnistuu alustallamme, jossa on työkalut kohdeyleisösi tavoittamiseen ja merkityksellisten vastausten saamiseen.
Kerää oikeat tiedot
SurveyMonkey tarjoaa työkalut, joilla voit tehdä, optimoida ja jakaa kyselytutkimuksia, jotta saat tarvitsemasi vastaukset.